What is sudoku and why is it so popular

Sudoku is a logic-based puzzle game that has become extremely popular in recent years. The objective of the game is to fill a 9×9 grid with numbers so that each row, column, and 3×3 sub-grid contains all of the digits from 1 to 9. Although this may sound relatively simple, the challenge lies in the fact that each puzzle has only one unique solution. Sudoku can be played online or in print, and there are numerous books and apps dedicated to the game. Many people find Sudoku to be an enjoyable and addictive pastime, as it provides a mental challenge and can be played at any time and anywhere.

The basics of how to solve sudoku puzzles

The first thing to understand about sudoku is that there is no guessing involved. Every single number must be placed logically as a result of deduction. With this in mind, let’s take a look at some basic sudoku solving tips:

Look for numbers that can only go in one place: if you see a number that can only fit into one slot on the sudoku grid, then it goes there! For example, if the only possible place for the number 1 is in the middle of a row, then that’s where it goes.

Make lists of what numbers can go where: as you fill in numbers on the sudoku grid, keep a running list of which numbers are still available for each row, column and 3

How to use backtracking algorithms to solve sudoku puzzles

Sudoku is a great game for developing your logic skills. And what better way to hone your logic skills than by using backtracking algorithms? A backtracking algorithm is a method of solving a problem by trying every possible solution until you find the correct one. So, how can you use backtracking algorithms to solve Sudoku puzzles?

First, you need to understand the basic rules of Sudoku. Every Sudoku puzzle has a unique solution, and you can solve it by using deduction and logic. There are no guessing or random elements involved. Second, you need to familiarize yourself with the backtracking algorithm. The best way to do this is to work through an example.

Write a sudoku solver in javascript using backtracking algorithms

Now that you understand the basics of sudoku and backtracking algorithms, it’s time to put your skills to the test! In this section, we’ll walk you through how to write a sudoku solver in typescript using backtracking algorithms.

The sudoku board

The sudoku board will be stored in a variable that has array of number array type.

We will create a sudokuBoard.ts file containing our board :

export const board = [
    [0, 0, 0, 0, 0, 0, 7, 2, 0],
    [9, 0, 0, 0, 4, 0, 0, 0, 1],
    [8, 0, 0, 7, 0, 0, 0, 4, 0],
    [0, 5, 0, 0, 3, 0, 0, 0, 8],
    [0, 6, 0, 1, 0, 0, 5, 0, 2],
    [0, 2, 0, 0, 7, 0, 0, 0, 0],
    [3, 0, 0, 0, 1, 0, 0, 0, 5],
    [0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 8, 0, 0, 0, 6, 0, 0, 4],
];

The required functions

We will need some functions to check values and solve the board.

Let’s create a sudoku.ts file in the same folder and import the board from the sudokuBoard.ts file :

import { board } from './sudokuBoard';

Now we will need several functions to :

• find the next empty spot
• check a value in a row
• check a value in a column
• check a value in a 9 squared box
  

And we will need some types :

• board type (array of numbers array)
• empty spot type (array of 2 numbers as coordinates)
  

First, add the types to the sudoku.ts file:

import { board } from './sudokuBoard';

type TBoard = number[][];
type TEmptySpot = [number, number];

Then the function that will take a board variable as parameter, and find the next empty spot (with 0 as value). If no empty spot is found, the function will return [-1, -1]:

import { board } from './sudokuBoard';

type TBoard = number[][];
type TEmptySpot = [number, number];

const nextEmptySpot = (board: TBoard): TEmptySpot => {
  for (var i = 0; i < 9; i++) {
    for (var j = 0; j < 9; j++) {
      if (board[i][j] === 0) return [i, j];
    }
  }
  return [-1, -1];
};

Now that we can locate an empty spot, we need to be able to test if a value can fit here. For that the value must be unique in the row, in the column and in the 9 squared box. We will check if this is true based on the value to test and the coordinates of the empty spot.

const checkRow = (
  board: TBoard, 
  row: number, 
  value: number
): boolean => {
  for (let i = 0; i < board[row].length; i++) {
    if (board[row][i] === value) {
      return false;
    }
  }

  return true;
};

const checkColumn = (
  board: TBoard, 
  column: number, 
  value: number
): boolean => {
  for (let i = 0; i < board.length; i++) {
    if (board[i][column] === value) {
      return false;
    }
  }

  return true;
};

const checkSquare = (
  board: TBoard,
  row: number,
  column: number,
  value: number
): boolean => {
  const boxRow: number = Math.floor(row / 3) * 3;
  const boxCol: number = Math.floor(column / 3) * 3;

  for (var r = 0; r < 3; r++) {
    for (var c = 0; c < 3; c++) {
      if (board[boxRow + r][boxCol + c] === value) return false;
    }
  }

  return true;
};

To use these 3 checking function at the same time, let’s factorize the call by creating a unique checkValue function :

const checkValue = (
  board: TBoard,
  row: number,
  column: number,
  value: number
): boolean => {
  if (
    checkRow(board, row, value) &&
    checkColumn(board, column, value) &&
    checkSquare(board, row, column, value)
  ) {
    return true;
  }

  return false;
};

So the file with all these functions should look like:

import { board } from './sudokuBoard';

type TBoard = number[][];
type TEmptySpot = [number, number];

const nextEmptySpot = (board: TBoard): TEmptySpot => {
  for (var i = 0; i < 9; i++) {
    for (var j = 0; j < 9; j++) {
      if (board[i][j] === 0) return [i, j];
    }
  }
  return [-1, -1];
};

const checkRow = (board: TBoard, row: number, value: number): boolean => {
  for (let i = 0; i < board[row].length; i++) {
    if (board[row][i] === value) {
      return false;
    }
  }

  return true;
};

const checkColumn = (board: TBoard, column: number, value: number): boolean => {
  for (let i = 0; i < board.length; i++) {
    if (board[i][column] === value) {
      return false;
    }
  }

  return true;
};

const checkSquare = (
  board: TBoard,
  row: number,
  column: number,
  value: number
): boolean => {
  const boxRow: number = Math.floor(row / 3) * 3;
  const boxCol: number = Math.floor(column / 3) * 3;

  for (var r = 0; r < 3; r++) {
    for (var c = 0; c < 3; c++) {
      if (board[boxRow + r][boxCol + c] === value) return false;
    }
  }

  return true;
};

const checkValue = (
  board: TBoard,
  row: number,
  column: number,
  value: number
): boolean => {
  if (
    checkRow(board, row, value) &&
    checkColumn(board, column, value) &&
    checkSquare(board, row, column, value)
  ) {
    return true;
  }

  return false;
};

The solving engine

We are close to the end of our sudoku solving program.

Now we will define the main process :

• step 1: find the next empty spot
• step 2: test all possible values by brute force (test from 1 to 9 whatever is already contained in the board)
• step 3: if a possible value is found, add it to the board and solve tis new board using recursion
• step 4: if the new board value can not be solved, get one step back, delete the value that was found at step 2 and try the next one (backtracking technique)
  

And here we go:

const solveSudoku = (board: TBoard): TBoard => {
  const emptySpot = nextEmptySpot(board);
  const row = emptySpot[0];
  const col = emptySpot[1];

  if (row === -1 && col === -1) {
    // board is full, return the solution
    return board;
  }

  for (let num = 1; num <= 9; num++) {
    if (checkValue(board, row, col, num)) {
      board[row][col] = num;
      solveSudoku(board);
    }
  }

  if (nextEmptySpot(board)[0] !== -1) board[row][col] = 0;

  return board;
};

And print the solution:

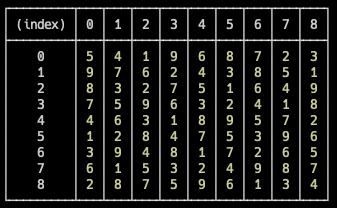
console.table(solveSudoku(board));

Final file and run

At the end of the day, you should have 2 files :

sudokuBoard.ts

export const board = [
    [0, 0, 0, 0, 0, 0, 7, 2, 0],
    [9, 0, 0, 0, 4, 0, 0, 0, 1],
    [8, 0, 0, 7, 0, 0, 0, 4, 0],
    [0, 5, 0, 0, 3, 0, 0, 0, 8],
    [0, 6, 0, 1, 0, 0, 5, 0, 2],
    [0, 2, 0, 0, 7, 0, 0, 0, 0],
    [3, 0, 0, 0, 1, 0, 0, 0, 5],
    [0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 8, 0, 0, 0, 6, 0, 0, 4],
];

sudoku.ts

import { board } from './sudokuBoard';

type TBoard = number[][];
type TEmptySpot = [number, number];

const nextEmptySpot = (board: TBoard): TEmptySpot => {
  for (var i = 0; i < 9; i++) {
    for (var j = 0; j < 9; j++) {
      if (board[i][j] === 0) return [i, j];
    }
  }
  return [-1, -1];
};

const checkRow = (board: TBoard, row: number, value: number): boolean => {
  for (let i = 0; i < board[row].length; i++) {
    if (board[row][i] === value) {
      return false;
    }
  }

  return true;
};

const checkColumn = (board: TBoard, column: number, value: number): boolean => {
  for (let i = 0; i < board.length; i++) {
    if (board[i][column] === value) {
      return false;
    }
  }

  return true;
};

const checkSquare = (
  board: TBoard,
  row: number,
  column: number,
  value: number
): boolean => {
  const boxRow: number = Math.floor(row / 3) * 3;
  const boxCol: number = Math.floor(column / 3) * 3;

  for (var r = 0; r < 3; r++) {
    for (var c = 0; c < 3; c++) {
      if (board[boxRow + r][boxCol + c] === value) return false;
    }
  }

  return true;
};

const checkValue = (
  board: TBoard,
  row: number,
  column: number,
  value: number
): boolean => {
  if (
    checkRow(board, row, value) &&
    checkColumn(board, column, value) &&
    checkSquare(board, row, column, value)
  ) {
    return true;
  }

  return false;
};

const solveSudoku = (board: TBoard): TBoard => {
  const emptySpot = nextEmptySpot(board);
  const row = emptySpot[0];
  const col = emptySpot[1];

  if (row === -1 && col === -1) {
    // board is full, return the solution
    return board;
  }

  for (let num = 1; num <= 9; num++) {
    if (checkValue(board, row, col, num)) {
      board[row][col] = num;
      solveSudoku(board);
    }
  }

  if (nextEmptySpot(board)[0] !== -1) board[row][col] = 0;

  return board;
};

console.table(solveSudoku(board));

Run the code

In the directory:

tsc sudoku.ts
node sudoku.js

Conclusion

Solving a sudoku board using the backtracking method is not so complex. The key is to understand how to cancel a non working value and test the next one.

The algorithm we wrote is working but could be improved :

• handle the case where no working value is found
• handle the ces where no solution exists
• test only possible values
• …

So it’s your turn now to take this code, play with it and improve it!

If you liked this article, maybe you could be interested by this one : How to use backtracking with javascript, and solve the n queens problem

Related articles

• Recursive functions with Javascript
• How to use backtracking with javascript, and solve the n queens problem
• How to improve the use of the console in javascript
  

What can you do to help me?

Please don’t hesitate to:

• Like the article
• Follow me
• Leave a comment and express your opinion.
  

Happy coding!