Backtracking is a general strategy that can be used to solve many different types of problems. It involves trying a series of possible solutions, and backtracking if necessary to try a different solution. backtracking can be used to solve problems like sudoku or the 8 queens problem.

To backtrack, you start by trying a possible solution. If it doesn’t work out, you backtrack to the previous step and try a different solution. You keep backtracking until you find a solution that works.

The n queens problem

The n queens problem is a classic example of a backtracking problem. The goal is to place n queens on a chessboard so that no two queens are attacking each other. This can be done by trying different possible solutions one at a time, and backtracking if necessary. The basic steps for solving the n queens problem using backtracking are:

1. Begin by placing one queen in any square on the board.
   
2. Check to see if any of the other queens on the board are attacking this queen. If they are, remove the queen from the board and place it in another square.
   
3. Repeat step 2 until you have either solved the problem or reached a point where there are no more possible solutions.
   

To translate this algorithm into javascript, we will need several tools :

sets: to store some values for further checks

functions to initialize the board and to check the other queen’s position

a solving function with backtracking

Result

We will declare an empty array to store all possible results of the problem:

const result = [];

Diagonals checking

For this exercise, we will have to check if Queens already exist in both diagonals: the positive diagonal and the negative diagonal.

Positive and negative diagonals are functions of rows and columns, so :

• positive diagonal = row number + column number
• negative diagonal = row number – column number
  

If we draw tables with both calculations, here is the result :

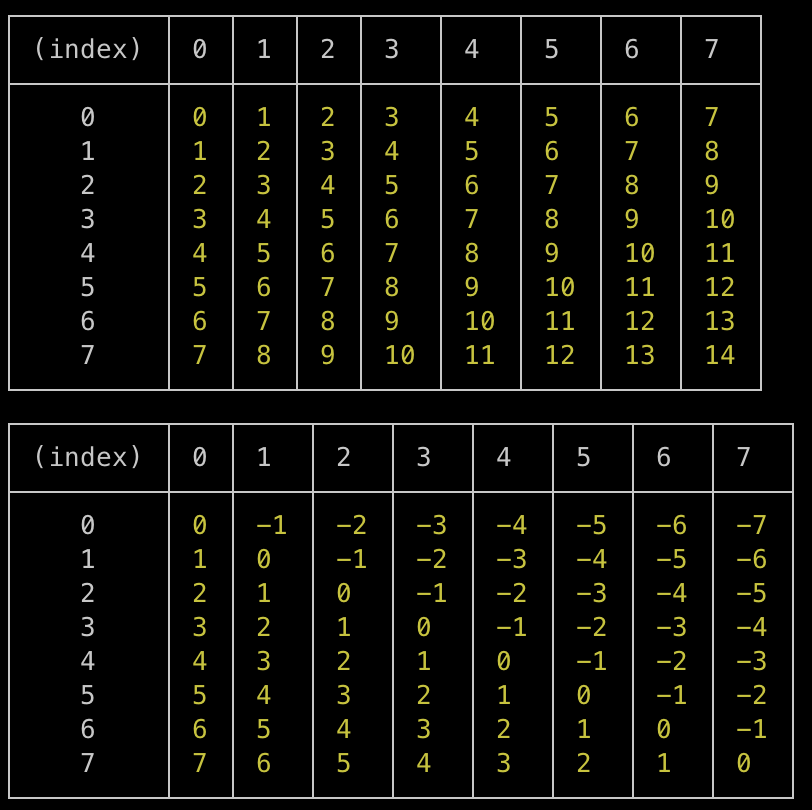
So if we store the values of the calculations, we can easily find if a queen is already on a diagonal.

Sets

We will use sets to store the values where queens are placed while we iterate each row :

• columns
• positive diagonals
• negative diagonals
  

const positiveDiagonal = new Set();
const negativeDiagonal = new Set();
const columns = new Set();

Functions

• Board initialisation
  

let board = Array(n)
  .fill('.') //fill to use map
  .map(() => Array(n).fill('.'));

• Push values in the sets and the result when a queen is placed
  

const setResult = (board, r, c) => {
  board[r][c] = 'Q';
  positiveDiagonal.add(r + c);
  negativeDiagonal.add(r - c);
  columns.add(c);
};

• Reset the last value: this is how we will erase the last value to try a new one during backtracking
  

const reset = (board, r, c) => {
    board[r][c] = '.'; // set the square to default
    positiveDiagonal.delete(r + c); 
    negativeDiagonal.delete(r - c);
    columns.delete(c);
  };

Solve the problem with backtracking

We have everything we need to start solving the problem.

We will place a queen, then place a second, and check row, column and diagonals if no other queens are attacking .

If there is another queen attacking, we place the queen in the next position, check again, and so on.

If we don’t find any position, we will go back to the previous queen, erase its position, and move it to the next position, and again if we can not find any satisfying position, go back to the previous one until we can find one possible solution.

This process is backtracking.

As we loop on all values, the output will display all possible solutions.

Final code

const solveNQueens = (numberOfQueens) => {
  const result = [];
  const positiveDiagonal = new Set();
  const negativeDiagonal = new Set();
  const columns = new Set();

  // we fill the board with dots
  let board = Array(numberOfQueens)
    .fill('.')
    .map(() => Array(numberOfQueens).fill('.'));

  const setResult = (board, boardRow, boardColumn) => {
    board[boardRow][boardColumn] = 'Q';
    positiveDiagonal.add(boardRow + boardColumn);
    negativeDiagonal.add(boardRow - boardColumn);
    columns.add(boardColumn);
  };

  const reset = (board, boardRow, boardColumn) => {
    board[boardRow][boardColumn] = '.';
    positiveDiagonal.delete(boardRow + boardColumn);
    negativeDiagonal.delete(boardRow - boardColumn);
    columns.delete(boardColumn);
  };

  const solve = (boardRow) => {
    if (boardRow === numberOfQueens) {
	//all rows are done, save the result in the result array
      const copiedBoard = board.map((row) => row.join(''));
      result.push(copiedBoard);
      return;
    }
    for (let boardColumn = 0; boardColumn < numberOfQueens; boardColumn++) {
      if (
        columns.has(boardColumn) ||
        negativeDiagonal.has(boardRow - boardColumn) ||
        positiveDiagonal.has(boardRow + boardColumn)
      ) {
        continue;
      }
      setResult(board, boardRow, boardColumn);

      solve(boardRow + 1);

      // After a solution, reset board and sets
      reset(board, boardRow, boardColumn);
    }
  };
  solve(0);
  return result;
};

console.log(solveNQueens(8));

Conclusion

The backtracking algorithm is a technique used to solve dynamic programming problems. This article discussed how backtracking can be applied in javascript, with the example of solving the 8 queens problem. The backtracking method is an effective way to find possible solutions when you have a set of constraints that need to be fulfilled.

You might also try applying this approach to solve Sudoku puzzles.

What can you do to help me?

Please don’t hesitate to:

• Like the article
• Follow me
• Leave a comment and express your opinion.
  

Happy coding!